Advances in Classifier-Free Guidance

Classifier-Free Guidance (CFG) has become the de-facto standard for steering diffusion models towards desired outputs. But what exactly does CFG do, and why does it work? In this post, we’ll first build intuition for CFG from the ground up, then explore two recent papers that shed new light on its inner workings and propose principled improvements.

Part 1: The Basics of Classifier-Free Guidance

The Problem: Conditional Generation

Diffusion models generate samples by iteratively denoising random noise. At each diffusion step $t$, the model predicts the noise $\epsilon_\theta(x_t)$ present in the current noisy sample $x_t$, which is then removed to obtain a slightly cleaner $x_{t-1}$.

For conditional generation (e.g., text-to-image), we want the model to generate samples that match a condition $c$. The model is therefore trained for conditional noise prediction $\epsilon_\theta(x_t, c)$.

However, if you sample from the trained conditional model, samples often lack fidelity and adherence to the provided condition.

Classifier-free guidance: The algorithm

Classifier-free guidance (CFG) is one approach to tackle this problem. Intuitively, we want the model to focus on realistic modes of the output distribution, accepting a potential loss of diversity. CFG combines conditional and unconditional predictions during inference, putting higher emphasis on the conditional prediction that is more likely to yield a realistic output:

$\hat{\epsilon}(x_t, c) = \epsilon_\theta(x_t) + s \cdot (\epsilon_\theta(x_t, c) - \epsilon_\theta(x_t))$

Here, $s$ is the guidance scale. Setting $s = 0$ gives the unconditional prediction alone; $s = 1$ yields the conditional prediction (so effectively the behaviour of the model doesn’t change), and $s > 1$ amplifies the influence of the conditional prediction.

The Distribution Perspective

That seems like a relatively hacky change, right? Well, let’s try to understand the impact on a theoretical level. From a probabilistic viewpoint, CFG can be interpreted as sampling from a sharpened conditional marginal distribution:

$\tilde{p}_t(x_t | c) \propto p_{\theta,t}(x_t) \cdot p_{\theta,t}(c | x_t)^s$

With $s > 1$, we concentrate probability mass on samples that more strongly satisfy the condition.

Text-to-image outputs without guidance (left) vs. with CFG (right). Without guidance, outputs often lack fidelity and adherence to the prompt. Source: [1]

Problems with CFG

While higher guidance scales often increase quality, generation also becomes increasingly unstable, resulting in outputs being distorted. In the case of image generation, this distortion can take the form of over-saturated images:

At high guidance scales, CFG can produce oversaturated colors and unrealistic artifacts. Source: [4]

This suggests a fundamental issue with CFG, where it might push the current noisy sample out of the model’s training distribution, so that the model does not know how to further denoise it. This occurs only for certain samples and can happen at any point during the denoising process.

Part 2 - Improving classifier-free guidance

The two papers we will discuss below both introduce a sample- and timestep-dependent adjustment to overcome these limitations. They use different assumptions as to how the ideal adjustment should look, however.

For certain dataset examples and conditions, our model might better approximate the true conditional distribution than for others. And as we theorize above, trajectories might become unstable only at certain points.

Foresight Guidance

Paper: Towards a Golden Classifier-Free Guidance Path via Foresight Fixed Point Iterations

The authors propose a simple criterion: At each denoising step, the ideal noisy sample $x_t$ is one that yields the same denoised result regardless of whether we use conditional or unconditional predictions.

The reasoning is that CFG is more stable and effective when unconditional and conditional predictions are similar. This allows the guidance to emphasize fidelity and prompt adherence without the confounding effect of a vastly different unconditional prediction.

Intuitively, if the prompt is “snowy mountains,” it is better if the unconditional prediction at each step points towards an output with mountains than, say, dogs. Then a conditional prediction pointing to snowy mountains would lead CFG to add more detail and snow, instead of changing the object altogether by adding some vector pointing from dogs to snowy mountains.

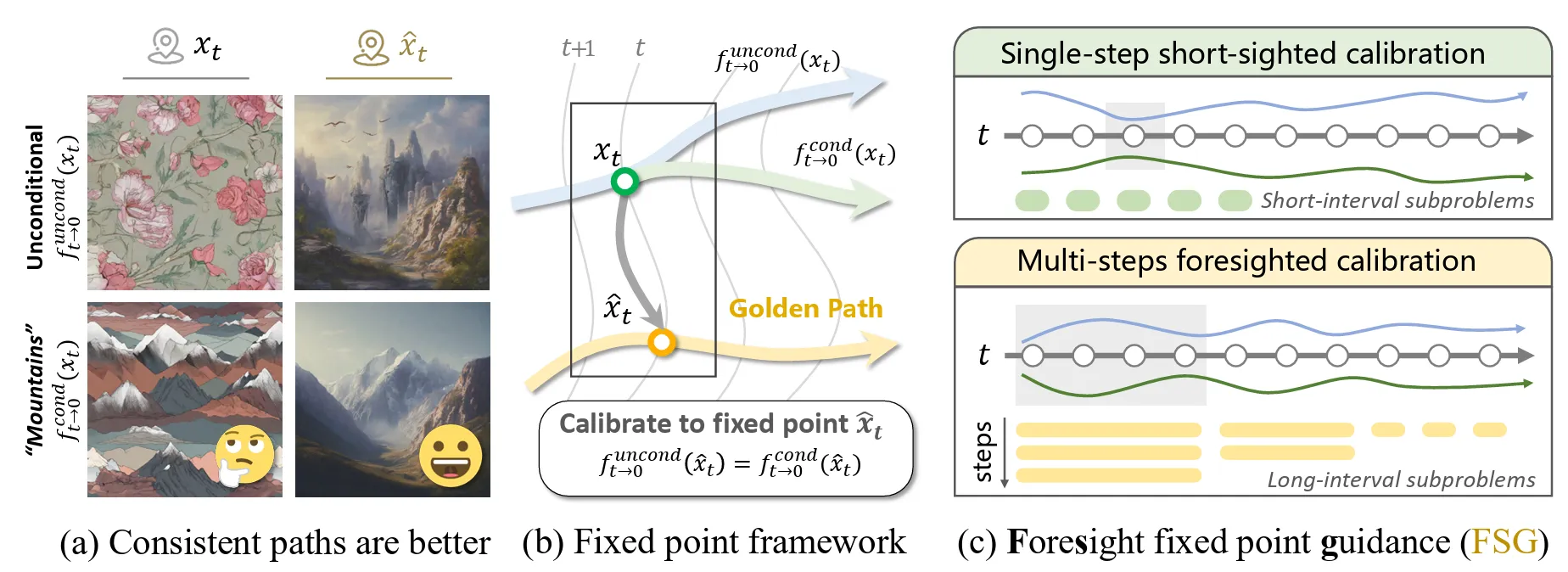
Foresight Guidance iteratively calibrates the noisy sample before each denoising step. Source: [2]

The proposed algorithm

To achieve this, the authors propose Foresight Guidance (FSG) that restructures each inference step into:

1. Calibration Step: Move the current noisy sample $x_t$ closer to the optimal $x_t^*$ (as defined by the consistency criterion above). This can be done iteratively using fixed-point iterations.

2. Denoising Step: Predict $x_{t-1}$ given the calibrated $x_t$.

Standard CFG performs essentially one calibration step per denoising step. FSG proposes a schedule where:

• Early in generation (high noise): Use more calibration iterations as prediction of the clean sample is more difficult, and important high-level structure needs to be created
• Later in generation (low noise): Fewer iterations suffice

This improves both image quality and computational efficiency compared to standard CFG.

Part 3: Feedback Guidance — Rethinking the Multiplicative Assumption

Paper: Feedback Guidance of Diffusion Models

In this paper, the authors identify an implicit assumption underlying CFG: that the learned conditional distribution is a multiplicative combination of the true conditional and unconditional distributions:

$p_\theta(x_t | c) \propto p(x_t | c) \cdot p(x_t)^\alpha$

This multiplicative structure in turn justifies CFG’s linear adjustment at each step in the diffusion space.

The paper proposes that the model’s conditional prediction is instead an additive mixture of true conditional and unconditional probabilities:

$p_\theta(x_t | c) = (1 - \beta) \cdot p(x_t | c) + \beta \cdot p(x_t)$

Why might this be more realistic? According to the authors:

The additive assumption… allows the learned conditional distribution $p_\theta(x_t|c)$ to be non-zero in regions where the true conditional distribution $p(x_t|c)$ is zero, a feat the multiplicative assumption is incapable of.

Intuitively, the learned conditional distribution is less precise and sparse in practice than desired, especially when some conditions are rarely seen in training or when the condition is not very informative.

From the additive assumption, the authors derive a state- and time-dependent dynamic guidance scale:

• When the current noisy sample $x_t$ appears unlikely to result in a sample fitting the condition, the guidance strength is increased
• When the sample trajectory already seems on track, guidance remains at a baseline (factor of 1)

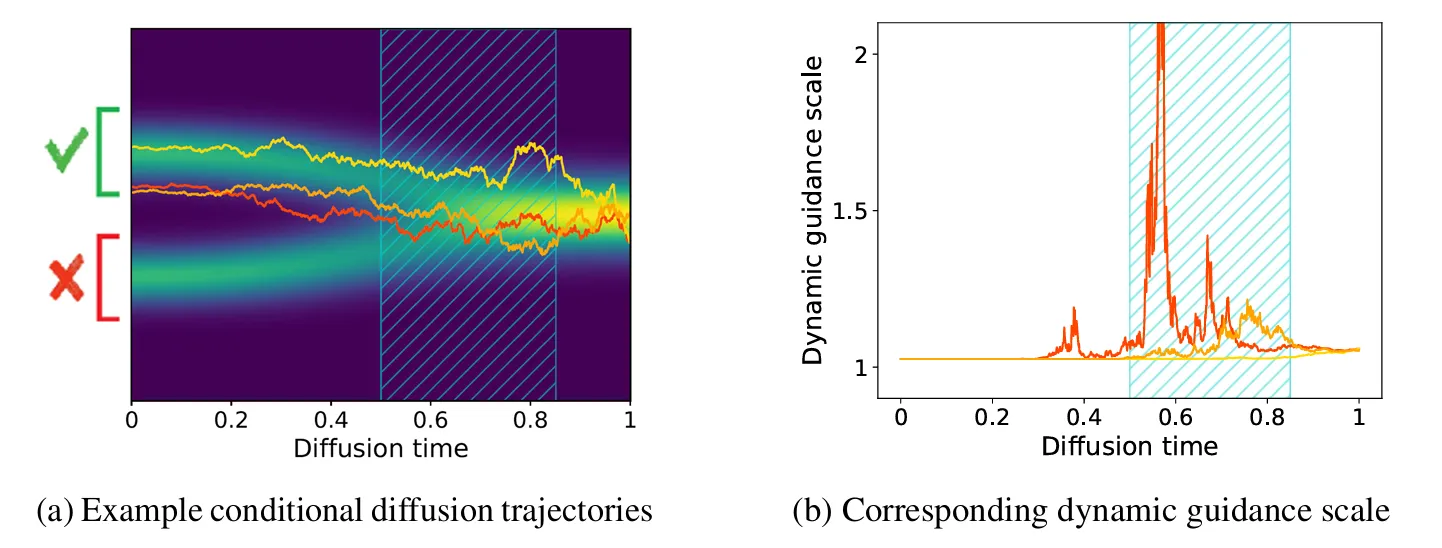
Feedback Guidance adapts the guidance strength based on the current sample’s likelihood of satisfying the condition. Source: [3]

On ImageNet, Feedback Guidance outperforms CFG and performs on par with Limited Interval Guidance (LIG).

Conclusion

CFG’s simplicity and performance have made it very popular, but these papers show there’s significant room for improvement by revisiting its underlying assumptions.

Foresight Guidance offers a unifying perspective where CFG is just one instantiation of a broader fixed-point framework, while Feedback Guidance challenges the multiplicative assumption at CFG’s core and derives a dynamic alternative.

Overall, sample-, diffusion-step-, and even noise-aware guidance appears helpful. In the future, it would be interesting to unify the two approaches discussed here, and perhaps to find a more theoretically grounded way of optimizing these approaches (perhaps we can train CFG hyper-parameters using some kind of adversarial loss on a validation set?).

References

1. Ho & Salimans (2022). Classifier-Free Diffusion Guidance
2. Wang et al. (2025). Towards a Golden Classifier-Free Guidance Path via Foresight Fixed Point Iterations
3. Koulischer et al. (2025). Feedback Guidance of Diffusion Models
4. Sadat et al. (2025). Eliminating Oversaturation and Artifacts of High Guidance Scales in Diffusion Models. ICLR 2025.