Bounded output regression with neural networks
Say we have a neural network (or some other model trainable with gradient descent) that performs supervised regression: For an input , it outputs one or more real values as prediction, and tries to get as close to a given target value as possible. We also know that the targets always lie in a certain interval .
This sounds like a very standard setting that should not pose any problems. But as we will see, it is not so obvious how to ensure the output of the network is always in the given interval, and that training based on stochastic gradient descent (SGD) is possible without issues.
Application: Directly output audio waveforms
This supervised regression occurs in many situations, such predicting a depth map from an image, or audio style transfer. We will take a look at the Wave-U-Net model that takes a music waveform as input , and predicts the individual instrument tracks directly as raw audio. Since audio amplitudes are usually represented as values in the range, I decided to use as the final activation function with as the last layer’s output at a given time-step. As a result, all outputs are now between -1 and 1.
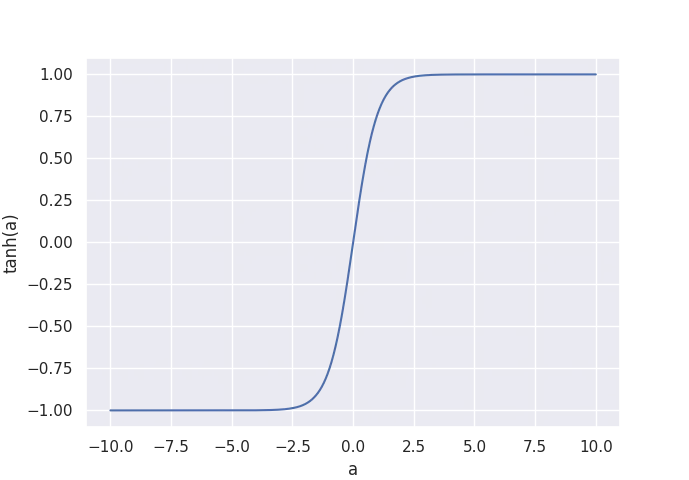
The function squashes all inputs to the range .
As loss function for the regression, I simply use the mean squared error (MSE, ) between the prediction and the target .
Squashing the output with : Issues
This looks like a good solution at first glance, since the network always produces valid outputs, so the output does not need to be post-processed. But there are two potential problems:
-
The true audio amplitudes are in the range , but and so never reaches -1 and 1 exactly. If our targets in the training data actually contain these values, the network is forced to output extremely large/small so that gets as close to -1 or 1 as possible. I tested this with the Wave-U-Net in an extreme scenario, where all target amplitudes are 1 for all inputs . After just a few training steps, activations in the layers began to explode to increase , which confirms that this can actually become a problem (although my training data is a bit unrealistic). And generally, the network has to drive up activations (and thus weights) to produce predictions with very high or low amplitudes, potentially making training more unstable.
-
At very small or large values, the gradient of with respect to a, , vanishes towards zero. At any point during training, a large weight update that makes all model outputs almost or would thus make the gradient of the loss with respect to the weights vanish towards zero, since it contains as one factor. This can actually happen in practice - some people reported to me that for their dataset, the Wave-U-Net suddenly diverged in this fashion after training stably for a long time, and then couldn’t recover.
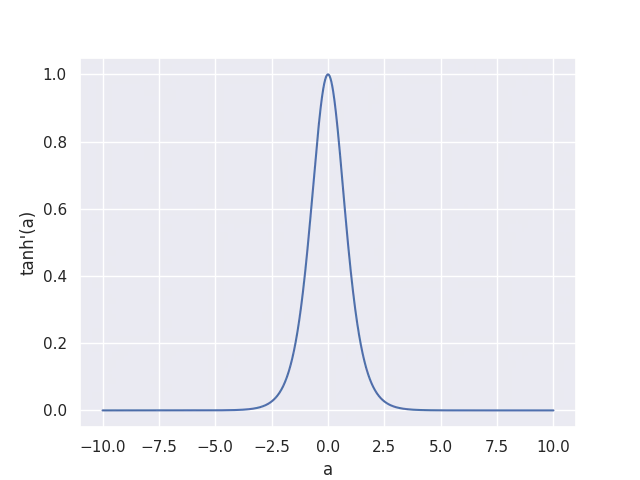
The derivative vanishes towards zero for large or small inputs, causing vanishing gradients.
Possible solutions
So what other options are there? One option is to simply use a linear output, but clipped to the range: . This solves problem number 1, since and can be output directly. However, problem number 2 still remains, and is maybe even more pronounced now: Clipping all output values outside means the gradient for these outputs is exactly zero, not just arbitrarily close to it like with , so the network might still diverge and never recover.
Finally, I want to propose a third option: A linear output that is unbounded during training (), but at test time, the output is clipped to . Compared to always clipping, there is now a significant, non-zero gradient for the network to learn from during training at all times: If the network predicts for example as amplitude where the target is , the MSE loss will result in the output being properly corrected towards .
I trained a Wave-U-Net variant for singing voice separation that uses this linear output with test-time clipping for each source independently. Apart from that, all settings are equal to the M5-HighSR model, which uses the function to predict the accompaniment, and outputs the difference between the input music and the predicted accompaniment signal as voice signal.
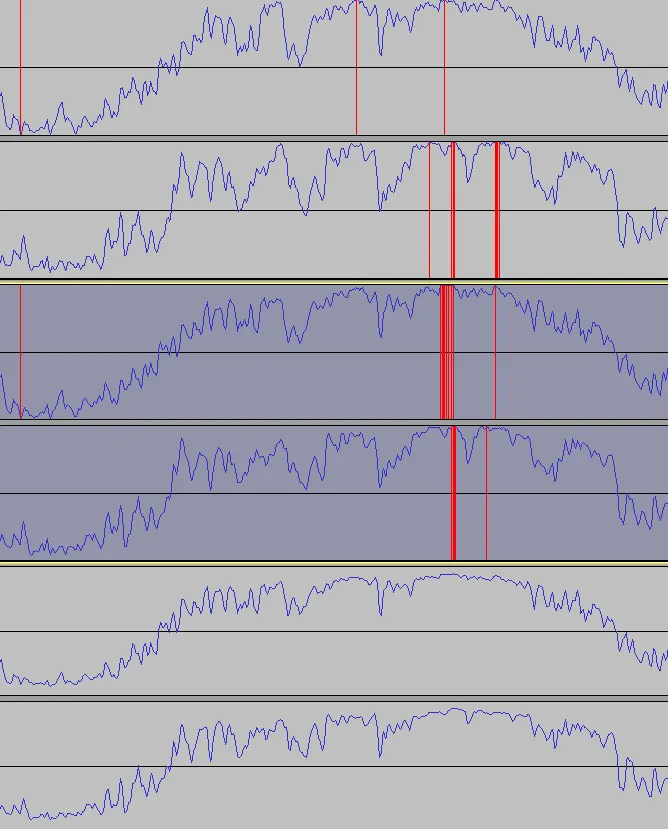
Comparison of output waveforms. The model (top) attenuates the signal, while our linear output model (bottom) preserves the full amplitude range.
We can see the accompaniment from the model is attenuated, since it cannot reach values close to and easily. In contrast, our model can output the input music almost 1:1, which is here since there are no vocals to subtract. The clipping occurs where the original input also has it, so this can be considered a feature, not a bug.
The problem with the accompaniment output also creates more noise in the vocal channel for the model, since it uses the difference signal as vocal output:
-
Original song
-
Tanh model vocal prediction
-
Linear output model vocal prediction
Outlook
Although we managed to get improvements over to output values of bounded range with neural networks, this might not be the perfect solution. Output activations such as or could also be considered, since they squash the output to a desired interval while still allowing to output the boundary values, but training might be difficult due to their periodic nature.
Also, different regression loss functions than MSE might be useful, too. If we used cross-entropy as loss function, it should provide a more well-behaved gradient even when using the activation, so different loss functions can also play a role and should be explored in the future.